非定常熱伝導解析では,時間微分項の離散化手法としてクランクニコルソン法と完全陰解法が一般的によく使用されます。
これらの手法は,陰解法であるのでタイムステップ dt の値をどのようにとっても,解が発散することはないと言われています。
前回は,完全陰解法について検討しましたが,今回は非定常熱伝導問題にクランクニコルソン法を使用して,タイムステップdtを変えて計算を行い,dt の解への影響について検討しました。
その結果,クランクニコルソン法は,dt が小さい場合は完全陰解法とほぼ同様の解が得られることを確認しました。
一方で,dt を大きく設定すると,数値振動が発生するため解が不安定になり定常解を求めることができなくなることを確認しました。
dt は,ある値以上になると数値振動の影響が大きく現われるため実用的には上限値があることを確認しました。
解析モデルは,例題 8 の温度拘束された 2 次元板の非定常熱伝導問題を使用しました。
時間方向の離散化は,後退差分近似を使用したクランクニコルソン法とします。
x = 0.020,y = 0.025 の点における温度の時刻歴を理論解と比較します。
計測点は,解析において温度の時間変化率が大きい点であることから決定しています。
計算はタイムステップの大きさを 0.01, 0.10, 1.00, 3.00 [sec] とした4ケースについて行ないました。
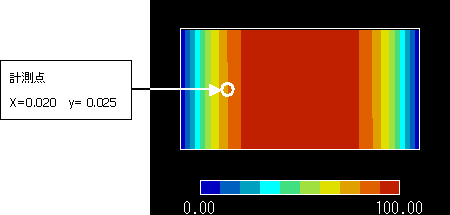
図 1 温度計測点(温度変化率が大きい点を選択しました)
図 2 に計算結果を示します。
dt を 0.01, 0.10 とした場合は,30.0 [sec] までの時間全域で理論解とほぼ一致しました。
dt を 1.00, 3.00 [sec] とした場合には,数値振動の影響が現われており計算精度が悪化しています。
特にdt を3.00 [sec] としたケースでは顕著に現われています。
これらの数値振動は,離散化手法に起因しているので,時間が十分経過したあとの解にも混入しています。
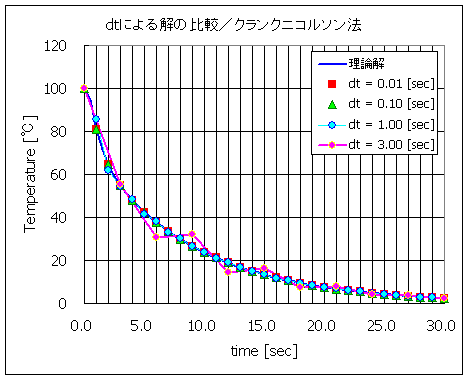
図 2 計算結果
以上より,クランクニコルソン法を使用した場合,時間増分値 dt がある程度の大きさまでであれば解が発散することなしに,計算解を得ることができることがわかりました。
しかしながら,dt をむやみに大きくすると離散化手法に起因する数値振動が顕著に現われてくるため,実用上 dt には上限があることが確認できました。
クランクニコルソン法と完全陰解法の解の精度について調べたところ,両者はほぼ同等の結果となりました。
本来,クランクニコルソン法は 2 次精度で,1 次精度の完全陰解法よりも高精度であることが特徴ですので,今回は問題が簡単過ぎたか,理論解を含めて数値計算上の誤差が大きかったのかもしれません。またコードの作成にも問題があるかもしれません。
いずれにせよ,今回の検証では,クランクニコルソン法が完全陰解法よりも解の精度が良いということを確認することはできませんでした。
なお,数値安定性に関しては次の文献が非常に詳細に説明していますので,興味のある方は一読してください。
藤井孝藏:「流体力学の数値計算法」,東京大学出版会
また次のサイトに詳細な説明が記述されています。
Internet-College of Finite Element Meshod http://www.fem.gr.jp/fem/index.html