図 1 に軸対称場の概要を示します。
軸対称場の座表系は r - θ - z のようにとります。
z軸を対称軸とすると円周方向すなわち θ 方向には物理量が変化しないことが仮定されます。
つまり,軸対称場では「温度」は円周方向に一定と仮定されます。
したがって,考慮するのは r - z 断面でよく,基本的には二次元場と同様に対処することができます。
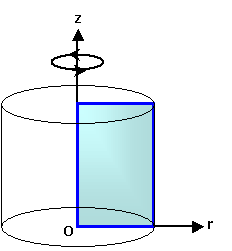
図1 軸対称モデル
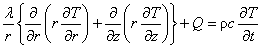
(1.1)
ここでは,境界辺上での境界条件の扱いについて説明します。
軸対称場では半径 r の環状要素を,z 軸を回転軸として回転させると考えます。
したがって,境界辺が回転軸に対して平行または垂直ではない場合は境界辺の r 座標が異なってくるため,境界条件の表現が二次元場の場合と完全に同じにはならないので注意が必要です。
ここで境界辺は長さが L の辺PQであり,辺PQが r 軸となす角を ψ とします。
2次元の時と同様の議論で,辺 PQ 上の任意点における温度に関して,節点 R の温度 TR の影響はゼロとなります。
すなわち辺 PQ 上の任意点における温度は節点 P 及び Q の影響のみを受けることがわかります。
一次要素において節点温度は節点間で線形近似されているので,辺 PQ 上の任意点での温度 T は次のように近似されるます。
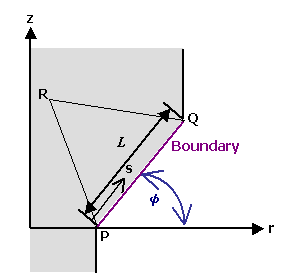
図2 境界辺を含む要素
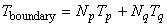
(1.2)
ここで,補間関数 N は次のように表されます。
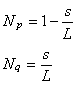
(1.3)
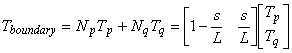
(1.4)
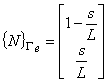
(1.5)
しかし中心軸において r = 0 となり,特異となるためこのままでは計算することができません。
そこで,一般的に次のような近似が用いらます。
すなわち「要素分割が十分妥当であり,要素が小さければ半径 r を要素の重心における半径 rc により代表させて近似できる」というもので,
次式のように近似します.
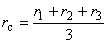
(1.6)
したがって,r に関する何らかの離散化式を近似しなくてはなりません。
そこで,一般的には三角形環状一次要素内の任意点 I における r 座標 ri は,次のように節点座標と内挿関数Nを用いて近似します。
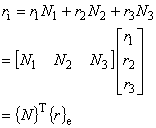
(1.7)
軸対称場では,境界辺上の任意点における r 座標は節点Pの r 座標を rp,線分 PQ と r 軸とのなす角を ψ とすると次式で表されます。
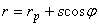
(1.8)
余弦の計算は図2を参照すれば次式のようになります。
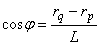
(1.9)
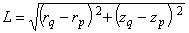
(1.10)
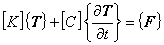
(1.11)
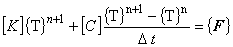
(1.12)
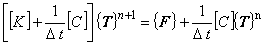
(1.13)
ただしその成分は異なっており,以下に各項の成分を示します。
[ k2 ],[ k3 ]の境界条件項の寄与は2次元問題と同じですのでそちらを参照下さい。
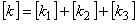
(1.14)
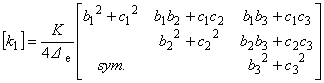
(1.15)
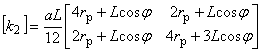
(1.16)
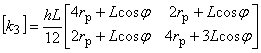
(1.17)
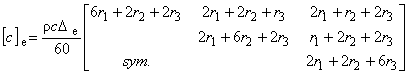
(1.18)
ここで L は境界辺の長さであり,rp は境界辺の始点での r 座標を表します。
{ f1 } は発熱項,{ f2 } は熱流速境界条件項, { f3 } は熱伝達境界条件項, { f4 } は熱輻射境界条件項となります。
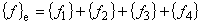
(1.19)
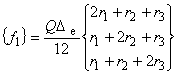
(1.20)
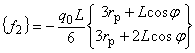
(1.21)
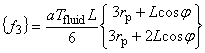
(1.22)
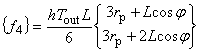
(1.23)