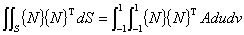
(3.1)
要素内の任意点でのポテンシャル値を,節点ポテンシャル値より補間する補間関数と,
要素の形状を表す形状関数に同じ関数を使用する要素のことです。
補間関数ベクトル {N} は,計算空間で使用されるので局所座標 p - q - r の関数で表現されています。
境界面は,局所座標系表示で必ず p , q , r のうちどれかが一定の面となります。
したがって,補間関数ベクトル {N} は,その一定値を代入すると変数が2つに減り,2 次元問題に帰着します。
例えば,次の図のような状況が一例として挙げられます。
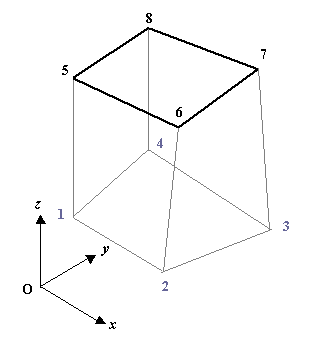
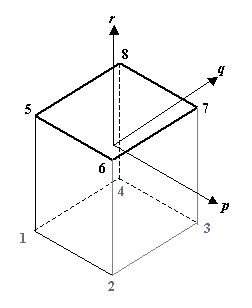
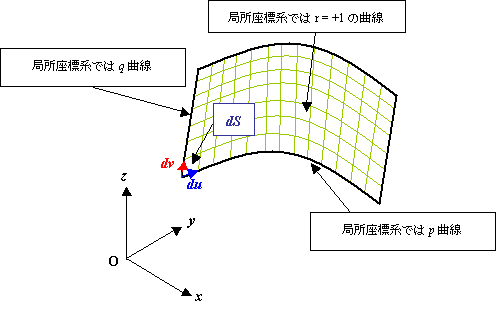
これは六面体 1 次要素の場合の境界面です。左図は物理空間(全体座標系)での形状であり,右図は計算空間(局所座標系)での要素形状を表します。
節点 5-6-7-8 で構成される面が境界面であり,局所座標系においては r = +1 一定の面となります。
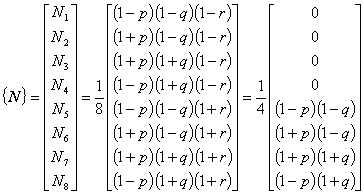
(3.2)
話を元に戻すと,境界積分項の数値積分において
物理空間の微小面積 dS と計算空間の Adudv の変換を求めておくことが必要になります。
つまり次式で dS と Adudv の関係を求めておく必要があります。
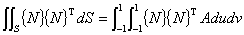
平面が曲面に包含されることを考えると,曲面の微小面積を求めるオペレーションを確立しておけば,平面の問題にも対応することができます。

曲面は平面を包含します。
しかしながら境界面が曲面の場合や平面でもねじれがあれば正確な計算が難しくなります。
そのような場合の常套手段として積分があります。
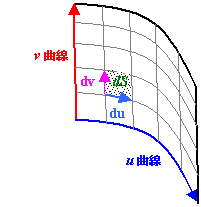
曲面を u と v からなる曲線座標により表現できるものとします。
またこの曲線座標に平行で互いに直交するような2つのベクトル du と dv により形成される四辺形領域の面積を dS とします。 du と dv を微小に,微小に持って行って考えると,やがて四辺形領域を平行四辺形とみなせるようになることが期待できます。 それに伴い,ベクトル du と dv の外積の大きさは,この平行四辺形の面積 dS を表すとみなせることになります。
曲面の面積を一度に計算することは困難ですが,領域を微小な四角形領域に分割すれば,四角形は平行四辺形で近似することができるようになるので,面積計算が容易になります。求まった面積を一個ずつ足し合わせていけば(積分すれば),曲面全体の面積を求めることができます。
つまり,ステーキを一度に食べるのはさすがに骨が折れますが,ナイフとフォークでステーキを切って食べやすくして食べるようなものと考えればよいでしょう。
式で表すと次のようになります。
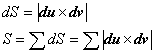
(3.3)
全体座標系での単位ベクトルを i , j , k とすると,
係数 ai , bi を用いて
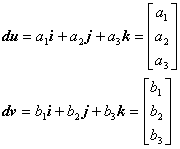
(3.4)
と表せます。
ではa,bはどのように表現できるのでしょうか。
duベクトルについて考えてみます。
duベクトルは微小な長さのベクトルです。
duについて,実際の計算は局所座標系で行うので,全体座標系表示を求めるのではなく,局所座標系表示を求める必要があります。
アイソパラメトリック要素では,全体座標と局所座標は補間関数 {N} と要素の節点座標 {x}e を用いて次のように補間されます。
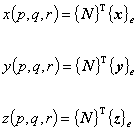
(3.5)
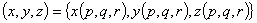
(3.6)
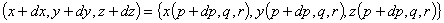
(3.7)
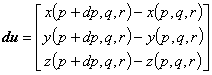
(3.8)
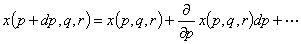
(3.9)
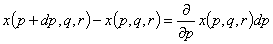
(3.10)
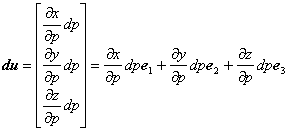
(3.11)
同様にして,q 曲線に沿うベクトル dv は以下のように表すことができます。
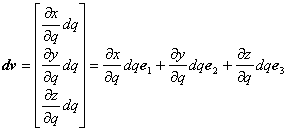
(3.12)
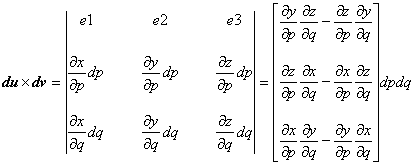
(3.13)
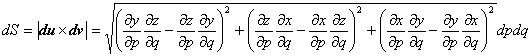
(3.14)
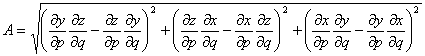
(3.15)
p または q が一定の面についても同様の手順で dS の変換式を求めることが可能です。