軸対称磁場解析 4 / 三角形環状 1 次要素の計算
　軸対称場において，2 次元場の三角形 1 次要素に対応する要素は三角形環状 1 次要素です。
この要素は，円筒座標系において r － z 平面における三角形 1 次要素を， z 軸を中心に回転させた要素と考えて下さい。
したがって，三角系環状 1 次要素の補間関数は，基本的に 2 次元場における三角形 1 次要素と同等です。
図 1 に三角形環状 1 次要素の概要を示します。

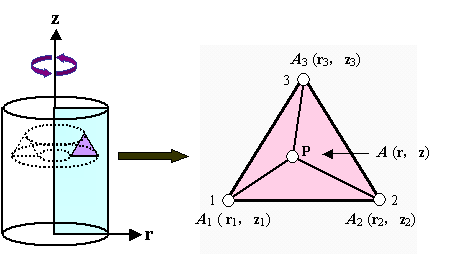
図 1 三角形環状 1 次要素
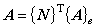
軸対称場において，要素内の任意点でのポテンシャル値 A は， 要素の節点でのポテンシャル値 {A}e及び内挿関数 {N} を用い 2次元場と同じように，次のように近似されます。
(4.1)
図 1 に示すように，三角形環状 1 次要素における各頂点のベクトルポテンシャルを， それぞれ A1，A2，A3とします。
ここで，要素内の任意点 P でのポテンシャル A を，未知係数を α1,α2,α3 として次のように 1 次式で近似します。
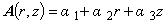
(4.2)
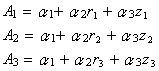
図1より各頂点での節点ポテンシャルについて次の 3 式が成り立ちます．
(4.3)
これをマトリックスで表現すると，
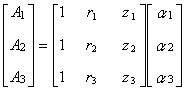
(4.4)
ここで逆行列の公式を使用して未知係数 α1,α2,α3を求めます．

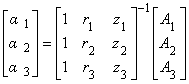
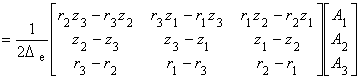
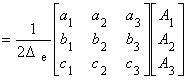
（4.5）
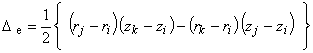
ここで，⊿e は r － z 断面における三角形要素の面積で，外積の計算により次のように表されます．
（4.6）
ここで，添字 i - j - k は循環する添字です．
また，
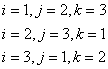
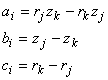
（4.7）
であり，添え字は式（4.6）で表されるものと同じです．
ここまでで未知係数が次のように求まりました．
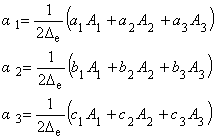
（4.8）
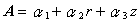
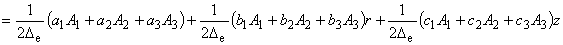
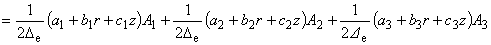
これを式(4.2)に代入すれば，要素内の任意点 P におけるベクトルポテンシャル A の値が求められ， 次のように表されます．

（4.9）
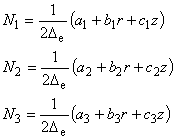
式(4.9)は，考え方を変えると要素内の任意点 P におけるベクトルポテンシャル A が 節点のポテンシャルによって表されることを示しています．ここで，
（4.10）
とおき，マトリックスで表すと，
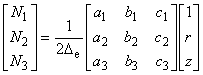
（4.11）
となります．
以上より，三角形環状 1 次要素において，その補間関数｛N｝は，2次元場の三角形 1 次要素と同等であることがわかりました．
また，三角形 1 次要素のところで説明したように， 形状関数と補間関数が等価であるため有限要素式の途中に現われる積分には，面積積分の公式が使用できます．