Math and Physics
ホーム > 数学と物理の予備知識 TOP > 数学と物理の予備知識 No.002
今回は，テーラー展開（Taylor Expansion）について頭に入れておくことを書いておきます。
テーラー展開を簡単に説明すると，「ある点 P ( x ) の関数値 f ( x ) が既知である場合に，点 P からみて ＋Δx のところの関数値 f ( x + Δx ) の値を f ( x ) をベースに関数近似するもの」と説明できます。
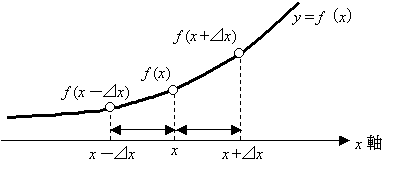
ここでテーラー展開の前提となる条件は以下のようになります。詳しい説明は大学の講義で使用する「微分・積分」の教科書を参照してください。図書館，古本屋，一般の書店，ネット通販，ネットオークション等で容易に入手可能です。
関数 f(x) の閉区間 a ≦ x ≦ b で n － 1 階の導関数が連続であること。
開区間 a ≦ x ≦ b で n 回微分可能であること。
変数を x とする関数 f ( x ) の値がわかっている場合，x から⊿x 離れたところでの関数 f ( x + ⊿x ）の値は，次のテーラー級数展開式で近似されます。
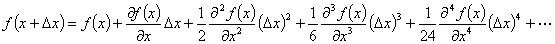
ここで，微分が含まれますが，偏微分ですので2次元問題であろうが3次元問題であろうが本質的には同じです。ちなみに，偏微分の記述で，
、 
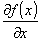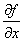、 f´
は同じことです。左が最も丁寧な書き方です。右側が最も簡便な書き方です。記述の仕方は人それぞれですが，意味は同じなので戸惑わないようにしましょう。ただし，2次元以上では偏微分する変数を明示する必要があるので，右側の表記は使うべきでありません。
ほとんどの教科書では，f ( x + Δx ) のテーラー展開について，「 f ( x ) を ⊿x まわりでテーラー展開すると～」と記述されていますが，いまいちピンと来ない表現です。
それよりも素直に，
「 x + ⊿x での ｆ の値をテーラー展開によって近似すると～」
と表現したほうがすっきりすると思えます。
テーラー展開を使う目的は， 変数を x とする関数 f (x) について，x + ⊿x あるいは x－⊿x というように間隔 ⊿x 移動した場合の関数値 f ( x + ⊿x ) を，既知の関数値 f (x)を使って近似しようということです。
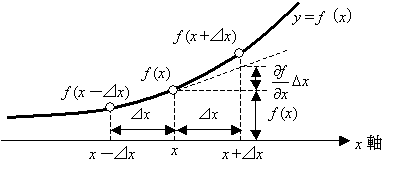
結論から述べると
１：項数を増やすと近似の精度が向上します。
２：⊿x の幅を十分小さくすると近似の精度が向上します。
例えば，
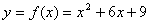
という初歩的な2次関数を考えます。この関数の x による偏微分は，1階の偏微分
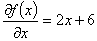
2階の偏微分
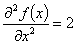
です。
では，テーラー展開を使って f (1) をベースに f (2) を近似して求めてみましょう。
刻み幅 ⊿x は 1 となります。
x = 2 を代入して計算すると正解は 25 であることがわかります。
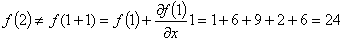
以上より誤差は
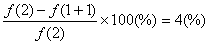
となります。
上の計算は１次の偏微分項まで導入した近似計算の結果です。
答えは実際の解と一致しません。
では2階微分項も考慮してみます。
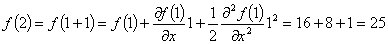
誤差は
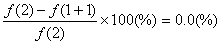
となり，テーラー展開による近似解は正解と一致します。このことは，高次の導関数の項を考慮するほど近似の精度が向上することを意味しています。
では次に高次の項を導入する変わりに，x の間隔 ⊿x を小さくした場合はどうなるでしょうか。
先ほどは⊿x は1でしたが，今度は 0.1 にしてみます。
つまりx = 1.1 の時の解を計算します。
まず関数の正解は
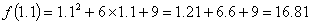
です。 2次近似すれば合うことは想像できます。したがってここでのポイントは1次近似でどれだけ正解に近づくかが焦点になります。
1次近似の場合
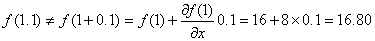
となり，誤差は
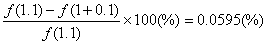
です。 予想通り近似解の誤差は，刻み幅を小さくすることで大きく減少しました。
ここで注目すべきことは2次近似と1次近似の差がほとんど無いということです。
2次の偏微分の項は極めて小さく無視してもよさそうであることがわかります。
これを一般論に解釈すると，
「間隔⊿xを，問題としている関数に対して十分小さくとれば，1次近似で十分な近似精度が得られる」
ということを示しています。
このことは，すべての近似解法に共通する重要なコンセプトです。
有限要素法であれば，節点の数を増やすことに相当します。
差分法であれば，格子点の数を増やすことに相当します。
観測点の間隔を小さくする。つまり観測点の数を増やすことで１次近似の定式化であっても近似の精度を上げることができるということです。したがってあとは計算機の処理能力の向上を期待すればよいのです。
以上の簡単な検討より，⊿xの幅を小さくすれば，2次以上の高次項は無視できると判断できるようになります。
この場合，テーラー展開は次のように簡略化されます。
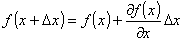
上の式は，ぱっと思いついただけでも
電磁気学での発散，
流体の質量保存則，
熱量の保存則，
ひずみの定義式，
応力の釣り合い
などを考える場面で登場します。
これらはいずれも有限要素法以前の各分野の基礎事項であり，テーラー展開をきちんと使えないと，有限要素法の勉強の手前で理解不能となってしまうことがわかります。
ところで偏導関数（偏微分）は x と x +⊿x の間の関数の勾配を表しています。
したがって，次のように式変形すれば，関数の具体的な形がわからなくても，
x と x + ⊿x での関数値がわかれば次のように偏微分を求めることができます。
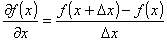
これは偏微分の前進差分近似です。 このように，差分公式はテーラー展開を自由に使えれば，覚えていなくてもその場で導出できるようになります。
