これらの手法は,陰解法であるのでタイムステップdtの値をどのようにとっても,解が発散することはないと言われています。
そこで,今回は非定常熱伝導問題に完全陰解法を使用し,タイムステップ dt を変えて計算を行い,dt の解への影響について確認しました。
その結果,今回の問題では,完全陰解法を使用した場合,dt を大きめに設定しても,数値的に不安定になることなく解が求まることを確認しました。しかしながら,dt が大きいと,温度変化率が大きい領域の解の精度が悪くなることがわかりました。
したがって,時間方向について,物理現象の解像度を上げるにはタイムステップ dt の大きさを小さくすることで解の精度が向上することを確認しました。
解析モデルは,例題 8 の温度拘束された 2 次元板の非定常熱伝導問題を使用しました。
時間方向の離散化は,1次精度の完全陰解法とします。
x = 0.020, y = 0.025 の点における温度の時刻歴を理論解と比較します。
計測点は,解析において温度の時間変化率が大きい点であることから決定しています。
計算はタイムステップの大きさを 0.01, 0.10, 1.00, 3.00 [sec]とした4ケースについて行ないました。
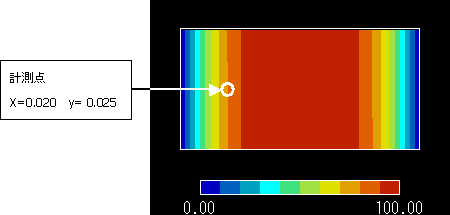
図1 温度計測点(温度変化率が大きい点を選択しました)
図2に計算結果を示します。
dt を 0.01, 0.10 とした場合は,30.0 [sec] までの時間全域で理論解とほぼ一致しました。
dt を 1.00, 3.00 [sec] とした場合には,時刻 0.0−10.0 [sec] 付近までの温度勾配が大きい領域で,誤差が目立ちます。
特に dt を 3.00 [sec] とした場合は誤差が大きくなりました。
この誤差は時間が経過するほど緩和され,十分時間が経過した後には dt をどのようにとっても理論解に近づくことが予想されます。
十分時間が経過した後の解というのは,定常解に他なりません。
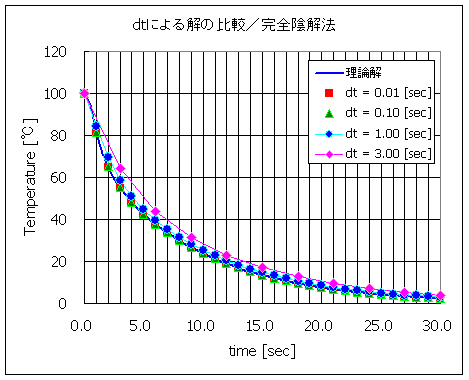
図2 計算結果
今回の検討により,完全陰解法を使用した場合,
「 時間増分値dt に依存して解が発散することなく,計算解を得ることができる」
ことがわかりました。
しかしながら,時間方向の解の精度を向上させるためには,dt をむやみに大きくすると誤差が大きくなることがわかりました。
これはスキームが 1 次精度であるからです。
時間方向の精度を上げるために dt をむやみに小さくすると計算ステップ数が増えるため,計算時間は増加します。
計算結果より,dt が大きい場合でも時間が経過し温度変化が小さくなってくると理論解と計算解との誤差は小さくなることがわかります。
すなわち,温度の時間変化率が大きい現象を精度良く追跡したい場合は,dt を適宜小さくすることが必要であり,定常状態に興味があり途中の計算時間を節約したい場合には,dt を大きくしても実用上は問題がなさそうであることがわかりました。
後者の判断が自分でできない場合には,計算時間は増加しますが dt を小さくして計算することを推奨します。
なお,数値安定性に関してはフォンノイマンの安定性解析という手法があり,次の文献で詳細に説明していますので,興味のある方は読んでみてください。
藤井孝藏:「流体力学の数値計算法」,東京大学出版会