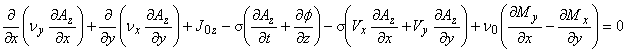
(7.1)
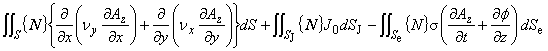
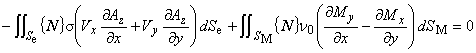
(7.2)
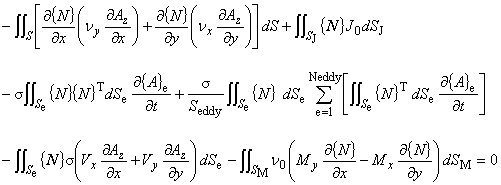
(7.3)
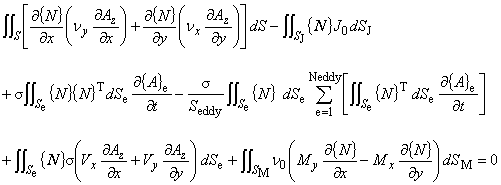
(7.4)
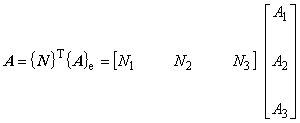
(7.5)
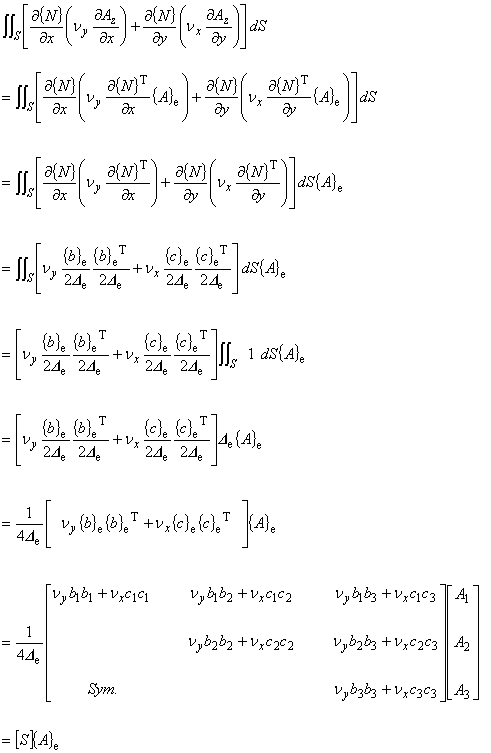
(7.6)
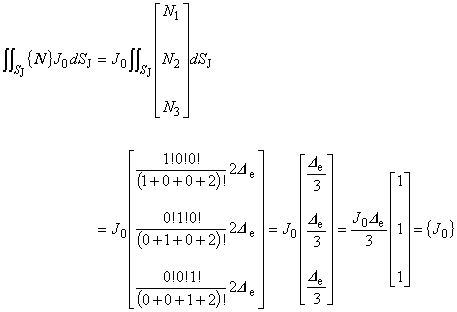
(7.7)
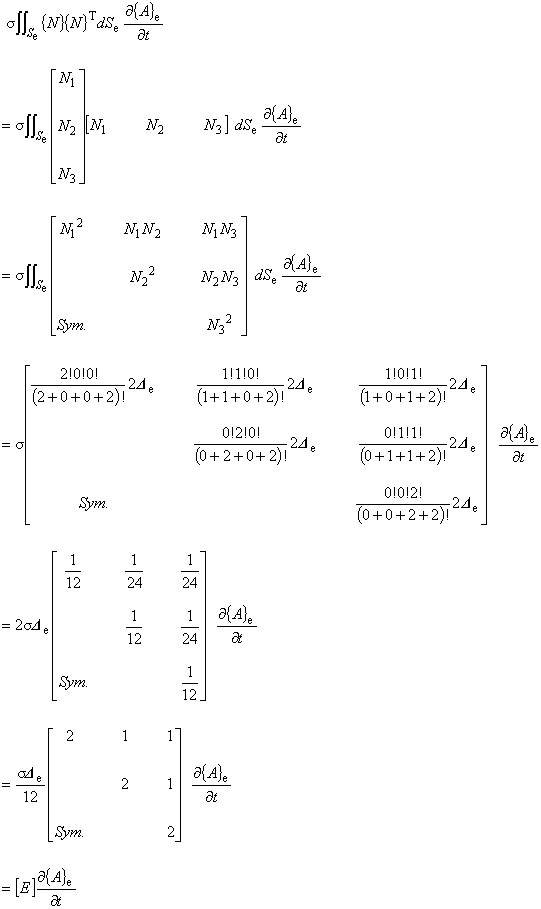
(7.8)
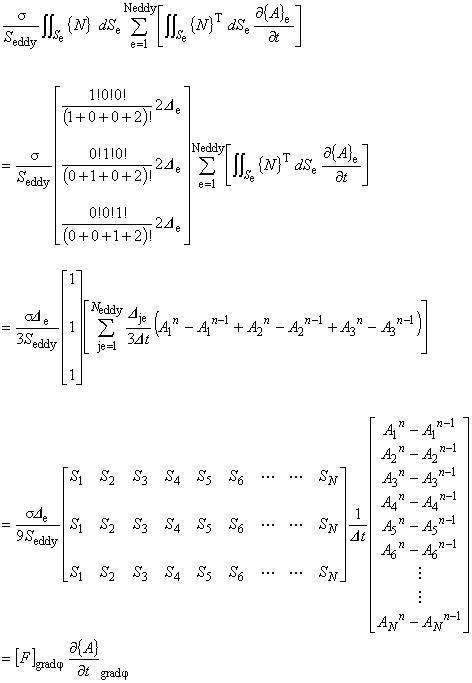
(7.9)
Sは渦電流を考慮する導体を構成する各節点を共有する要素の面積の和を示します。 詳細はNo.4を参照して下さい。
なお,この方法によるgradφの離散化は現在では一般的ではなく, gradφ自体を未知数とする手法がより一般的です。
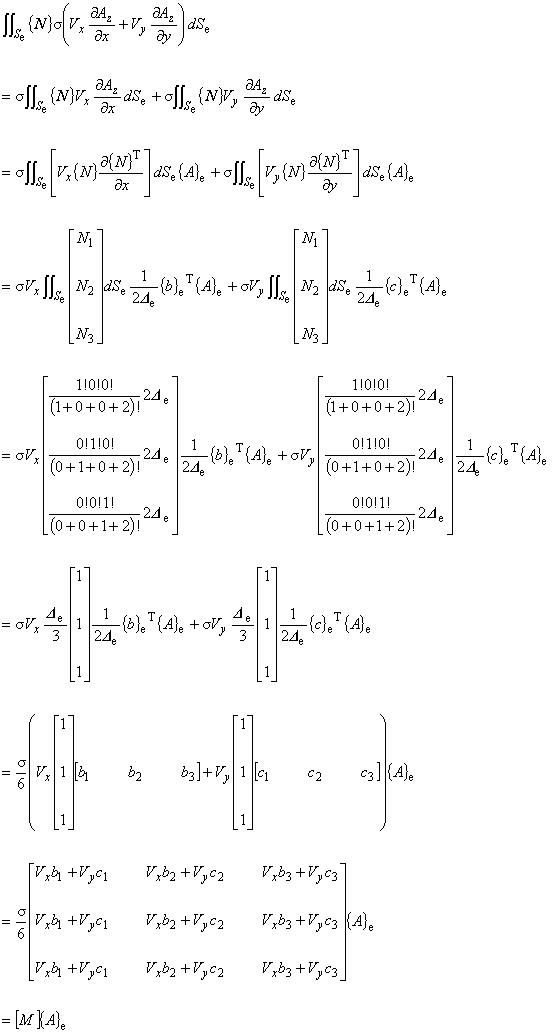
(7.10)
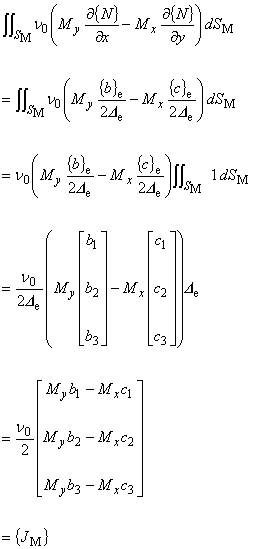
(7.11)
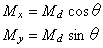
(7.12)
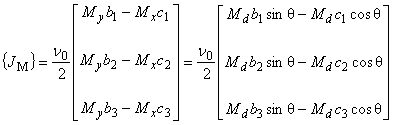
(7.13)
まず,弱形式化された式(7.4)を示します。
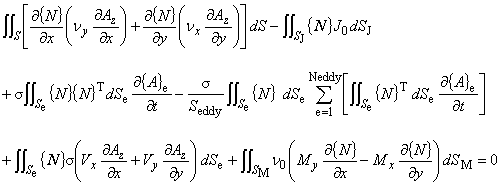
(7.4)
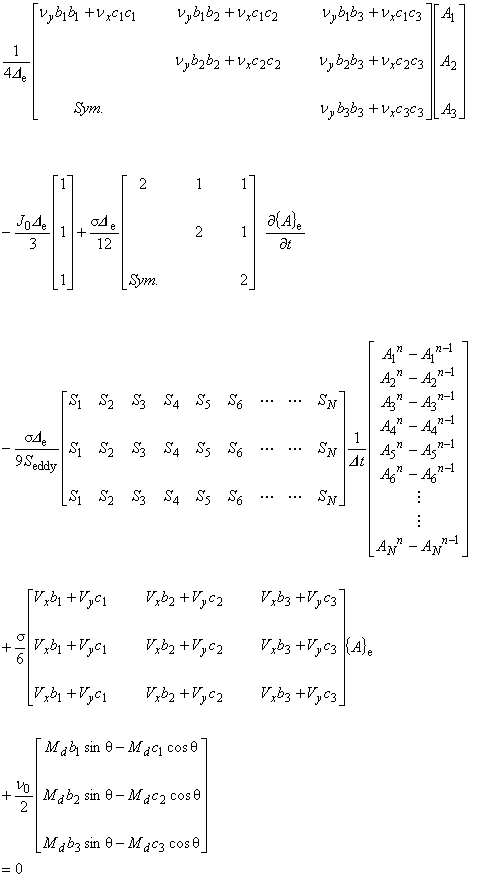
(7.14)
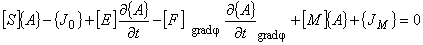
(7.15)
この式を解くことで線形問題を解析することができます。
三角形一次要素を使用した場合には,磁場 B [T] は次式で表されます。
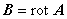
(7.16)
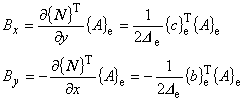
(7.17)
磁性体の磁気抵抗率 ν [m/H] や磁化 M [T] といった物理量は, B の関数であるため,これらの値も要素内で一定となります。
したがって,一次要素を用いる場合は,B が急激に変化する領域で, 十分細かく要素分割を行なうことが精度を保つ上で望ましいといえます。
なお,ν や M といった磁気特性の非線形性を考慮した解析を行うためには, Newton-Raphson法を視野に入れた離散化が必要となります。
その点については次回説明します。