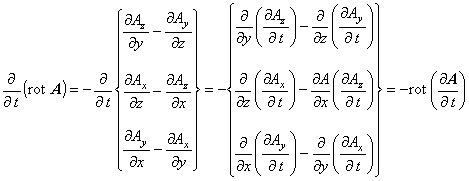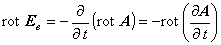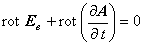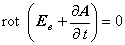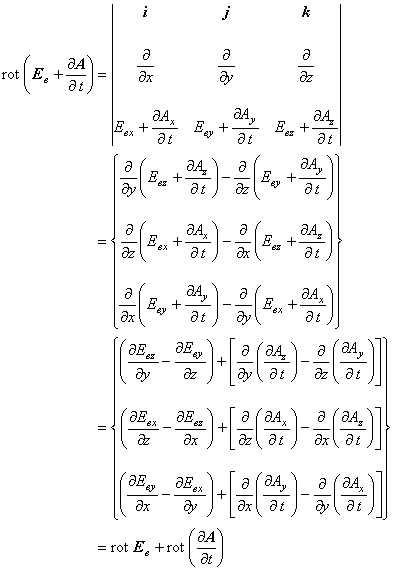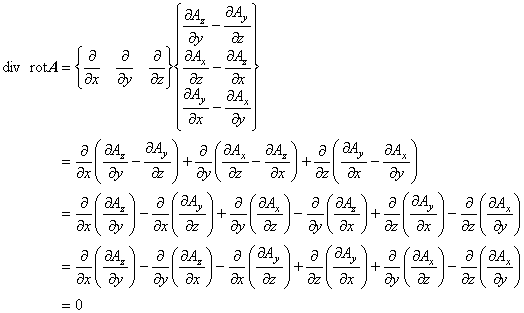
つまりここでは，
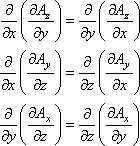
という関係に注意してください。
したがって，div rot A = 0 が成り立つことがわかりました。
A´ = A + grad φ
で定義されるベクトルポテンシャルの回転 rot A´ は，rot A であるから， ベクトル場はスカラーポテンシャル
φ の勾配の数だけ存在することがわかります。
このことは，以下の式変形から容易に導けます。 まず，ベクトルの回転場を分配すると次の式のように変形できます。
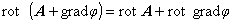
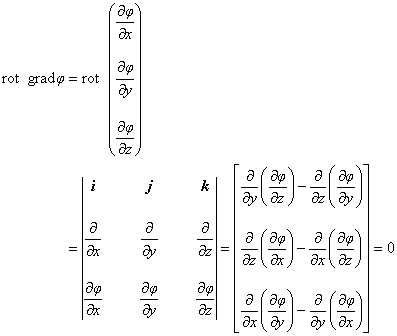
以上より
rot ( A + gradφ ) = rot A
が証明されました。
俗に言うと，z 方向について金太郎飴状態なわけです。
金太郎飴は，ｚ 断面である xy 平面における物理量に相当します。
ここでは，任意の z 断面で磁束密度 B は Bx , By の成分をもちます。
2次元場ですから z 方向に物理量は成分を持たないので Bz は 0 となります。
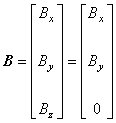
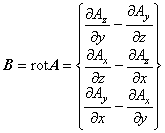
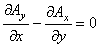
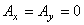
の場合です。
したがって，2次元の磁場問題ではベクトルポテンシャル A は ｚ 方向成分のみを有することがわかります。
磁場問題は，磁場 B [T] を求めることを目的としており，2次元問題では磁場 B は z 方向には成分を持たず
x , y 方向成分のみ有しています。
一方， B [T] のベクトルポテンシャル A は，このとき z 方向成分のみしか持ちません。
この点については一度式変形を行って確認してみて下さい。
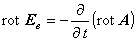（1.24） 
