Math and Physics
ホーム > 数学と物理の予備知識 TOP > 数学と物理の予備知識 No.007
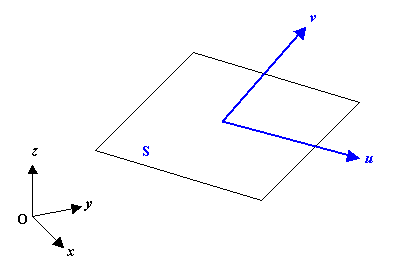
下の図は，ある平面 S の面内において局所座標系 u - v が定義されている様子を示しています。
面内というのは，「面上の」ということです。
面外というのは，「面にのっていない領域」を示します。一般的には「面に対して法線方向に対する領域」を指します。
つまり，面内であれば u - v 座標で定義されますが，面外となると u - v 座標では定義できません。
S は平面であり，2 次元空間であるのでこのことは自明であるといえます。
ところで，平面 S は関数により記述することができます。
高校の数学で幾何学や代数学などを勉強したときに出てきます。
どのような関数になるか詳細はわからなくても，関数を f とすると，変数は2つの軸である u と v により表現することができますので，
関数は f（u,v）と一般化して記述することが可能です。
ここで，f の詳細な唯一の式を求めさせるのが日本の高校までの教育です。
初めて勉強する場合にはそれでよいと思います。
しかし，専門色の強い学問ではそれではすぐに壁に当たってしまいます。
それは，議論を展開するために関数表現を用いることが多く，専門書などを読んで関数が出てきても，その詳細を知る必要は無い場合が多いのです。概念が理解できればいいという感じでしょうか。ですから出てきた関数の具体的な式がわからなくて悩んでいると，先へ進めなくなることが多いのです。
頭を切り替える必要がありますが，大学ではそのように考え方を変えるように説明する教官はわりと少ないのではないでしょうか。
また高校までの教育がテスト勉強のための教育なので，テスト用の問題として扱いやすい唯一の解を求めさせる作業になりやすく，思考の柔軟性を失わせる結果を招いています。
有限要素法などにしても，抽象的な数式展開が頻繁に出てきますので，抽象的な説明には具体的な式ではなくイメージで理解していくことがよいと思います。
S は必ずしも，平面である必要はありません。
あくまでも面という 2 次元空間であればよいからです。
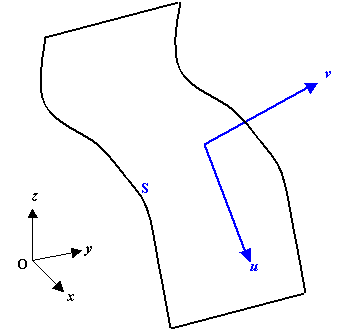
すると次のような曲面を想起することができます。
曲面を S とします。
曲面 S を表す関数を g とします。曲面 S も面ですので、平面のときと同様に、2つの変数で表される関数で表現できます。その変数を u,v とすれば， g（u,v） と記述することができます。
ただし，関数の具体的な数式については先と同様に追求しません。
ここでは，関数の内容を一意に求めることを問題としているわけではないからです。
この曲面 S 上の任意点における法線や法線ベクトルが必要になることが多々あります。
曲面 S 上の任意点 P における法線ベクトルを求めるためには，座標系１で説明したように
まず、任意点を含む平面を定義する必要があります。
曲面 S 上の任意点 P と、曲面 S 上の別の点 A を結ぶベクトル u を求めます。これは曲面 S 上の任意点 P における接線ベクトル uであるともいえます。
続いて、ベクトル u と直交するように、任意点 P と曲面 S 上の 点 A とは異なる点 B を結ぶベクトル v を求めます。これは曲面 S 上の任意点 P における接線ベクトル vであるともいえます。
曲面 S 上の任意点を通る 2 つ接線ベクトル u と v により任意点を含む平面が定義されますので、この 2 つのベクトルの外積ベクトル w = u × v は曲面 S の任意点における 法線ベクトル n であるといえます。
ここで 曲面 S に u , v 座標系のグリッドを追加して、上に述べたことをもう一度説明してみます。
考えやすければよいので，自分流にいろいろ補足してかまいません。
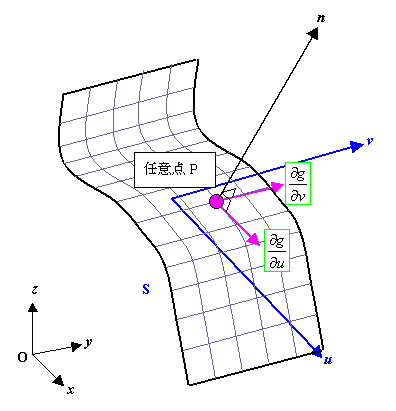
点 A を曲面 S 上のローカル座標系 u に沿う点とすれば、任意点 P と A を結ぶベクトルは、曲面 S 上の任意点 P における接線ベクトルを表し、この接線ベクトルは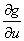 
と表されます。
これは曲面 S 上の任意点 P における ローカル座標軸 u 方向の勾配を現し、接線ベクトルそのものです。
点 B を曲面 S 上のローカル座標系 v に沿う点とすれば、任意点 P と B を結ぶベクトルは、曲面 S 上の任意点 P における接線ベクトルを表し、この接線ベクトルは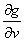 
と表されます。
これは曲面 S 上の任意点 P における ローカル座標軸 v 方向の勾配を現し、接線ベクトルそのものです。
ローカル座標系 u と v が直交するとすれば、上の 2 つの接線ベクトルは互いに直交します。
曲面 S 上の任意点 P と 曲面 S 上の点 A および B の 3 点の間隔を微小にとれば，P と A , B により作られる 2 つのベクトル は，任意点 P を含む平面の接線ベクトルを表します。
曲面 S 上の任意点 P における 2 つの互いに直交する接線ベクトル 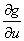と 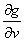の外積ベクトルは，この 2 つの接線ベクトルに対してそれぞれ直交するベクトルを表し、これは任意点 P における法線ベクトル n といえます。したがって、法線ベクトル n は、以下のように求められます。
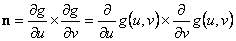
法線ベクトル n は単位長さあたりのベクトルであるので，その大きさ n は
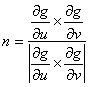
と求めることができます。 点 P が尖がっている面の先端部分ですと，接線が無数に定義されるので法線方向を一意に定めることができません。このような点を特異点とよびます。
以上で座標系の２回目を終わります。
