
 Math and Physics
Math and Physics
ホーム > 数学と物理の予備知識 TOP > 数学と物理の予備知識 No.008
数値解析による非線形問題の解法として最も一般的な方法にニュートンラプソン法というものがあります。
この方法は,多くの教科書に記載されていますので,勉強した人も多いと思います。
数値計算では,非線形解が得られたことを「収束解が得られた」であるとか「解が収束した」などと言います。
常に収束解が得られればそれに越したことはありませんが,そうも行かないのが現実です。
一般に汎用数値計算ソフトウェアでは非線形解法にさまざまなパラメータが用意されています。
収束しない場合は,計算が収束できるようにパラメータをいろいろ動かしてゴリゴリ,トライアンドエラーを行わなくてはなりません。が悲しいことになかなかうまく解が得られないことが多々あります。
ここで,収束しない状況には大きく分けて 4 つのケースがあります。
1:ユーザーによる問題設定が不適切であるケース
2:モデル化には問題はないものの,ユーザーが定義した解析条件に問題があるケース
3:計算コードの守備範囲を超えた設定の問題を解こうとしている
4:データの設定も適切かつソフトの守備範囲内であるが,収束解を得るのにシビアな問題
収束解が得られない場合,上記のどれに起因しているのかをひとつずつ検証していく必要があります。
筆者が仕事で使用している LS-DYNA というソフトウェアでは,静的な問題を陰解法により解くことがよくあり,単純には収束しない問題を収束させるためのコツがあります。この辺はソフトウェアごとに異なりますし,問題によっても随分違うはずです。LS-DYNAでは大きく変形する大変形問題や大きく変位する大変位問題を頻繁に扱いますが,問題のタイプによって収束解を得るためのポイントが異なります。なかには上記の 1 と 2 の見極めが難しく収束解を得ることに苦労する場合もありますが,適切にモデル化された問題の多くは収束解を得ることができます。(経験談)
ここでは,収束計算プロセスの骨格であるニュートンラプソン法について勉強してみましょう。プロセスがわかっただけで実務の解析がうまくなる保証はありませんが,勉強するチャンスと考えて知っておくとよいでしょう。
図 1 に示す最もシンプルな関数形が既知である一変数問題のニュートンラプソン法を勉強します。
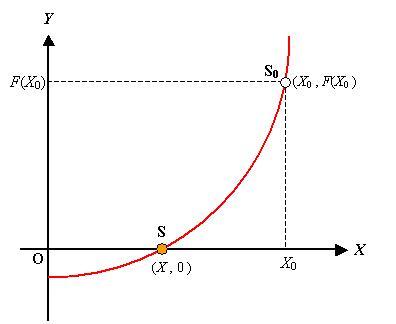
図 1 1 変数問題
この問題は,初期値として我々は関数
|
(8.1) |
にいるとし,ここから,
|
(8.2) |
を満たす X をニュートンラプソン法により求めることです。
しかし我々は最終目標として関数形が未知の問題を解かねばなりません。
そのためには関数形が既知であることを前提とした解法は通用せず,関数形が未知の場合でも求解できるニュートン・ラプソン法のような手法が必要となります。
この問題のミソは, Y を与えて,それを満たす X という解を得ようとしていることです。
その逆は, X を与えてそれを満たす Y という解を得ることです。
少し勉強されている方ならこのことが意味していることは直ぐに分かるかと思います。
ニュートン・ラプソン法を簡単に言うと,初期状態 S0 から Taylor展開による近似を繰り返し行ない,X0 から漸次 X に接近して解を見出そうとするものです。
であるならば,二分法でもよいではないかという声がありますが,それでは CPU TIME がかかるのです。
我々は大規模な問題を短時間で効率よく解きたいと思っています。
そのためには初期値がある程度いい加減な状態でもすぐに収束解を見出せる解法が必要です。
その代表的なものがニュートンラプソン法なのです。
関数形が既知であるので, S0 から dX0 離れた点における関数値は,Taylor 展開によれば次のように見積もることが可能です。
|
(8.3) |
簡略化のために高次項を無視すると,
|
(8.4) |
となります。 ここで,左辺は目標としている関数値であり,S において
|
(8.5) |
となります。
したがって,X の増分値
|
(8.6) |
が得られます。
これにより,初期の解 X0 よりも dX0 だけ真解 X に近づいた更新された近似解 X1 の値が
|
(8.7) |
として得られます。
したがって,関数形が既知であるので直ちに,X1 に対応する関数値 F ( X1 ) が求まります。
この点を S1 とします。
図 2 を見て,我々は S0 からゴール S を目指して S1 まで来たことを理解して下さい。
当然まだ S との差(誤差)があり,数値計算でいう解が収束した段階ではなく反復計算中ということになります。
この差が,ユーザーが設定した許容値ε以下になれば真解が得られたとみなします。
|
(8.8) |
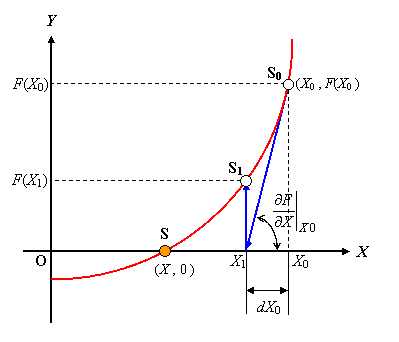
図 2 1 回目の試行計算により S1 が見出された!
まだ解は収束していませんので,次の近似解を得るべく計算を続行します。
点 S1 において dX1 離れた点における関数値はTaylor展開によれば次のように見積もることが可能です。
|
(8.9) |
簡略化のために高次項を無視すると,
|
(8.10) |
となります。
ここで,左辺は目標としている関数値であり,S において
|
(8.11) |
となります。 したがって,
|
(8.12) |
が得られます。
これにより,現在の近似解 X1 よりも dX1 だけ真解 X に近づいた近似解 X2 の値が
|
(8.13) |
として得られます。
したがって,関数形が既知であるので直ちに,X2 に対応する関数値 F(X2) が求まります。
この点を S2 とします。
図 3 を見て,我々は S0 からゴール S を目指して S2 まで来たことを理解して下さい。
当然まだ S との差(誤差)があり,数値計算でいう解が収束した段階ではなく反復計算中ということになります。
この差が,ユーザーが設定した許容値 ε 以下になれば真解が得られたとみなします。
|
(8.14) |
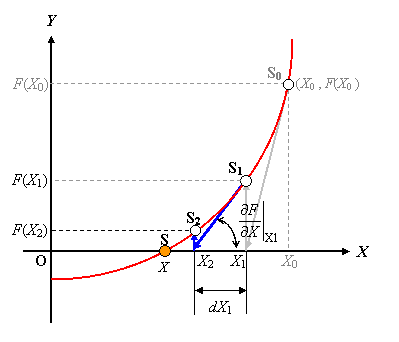
図 3 試行計算により S2 が見いだされた!
図ではまだ解が求まっていません。
別な言い方をすれば,解は収束していません。
したがって,さらにニュートンラプソン法による反復計算を続行していきます。
以上のプロセスにより,解の変化が指定した許容値以内に収まった時点で,解は収束したとみなします。
実際の非線形 CAE 計算では,解が収束値へ単調に向かうことばかりでなく,誤差が減少したり増加したりを繰り返すことも珍しくありませんが,ニュートン・ラプソン法の直感的な理解としては上のプロセスを繰り返して許容誤差(トレランス)以下に解が落ち着いた時点で収束とします。